When we talk about probability, we often think of it as a simple concept. For instance, the probability of getting heads on a coin toss is 50%, or the probability of rolling a six on a standard die is 1/6. However, in many situations, the probability of an event can depend on more than one factor. This is where the concept of compound probability comes into play. This article will explore the basics of understanding compound probability and learn how to calculate it in different scenarios.
What is Compound Probability?
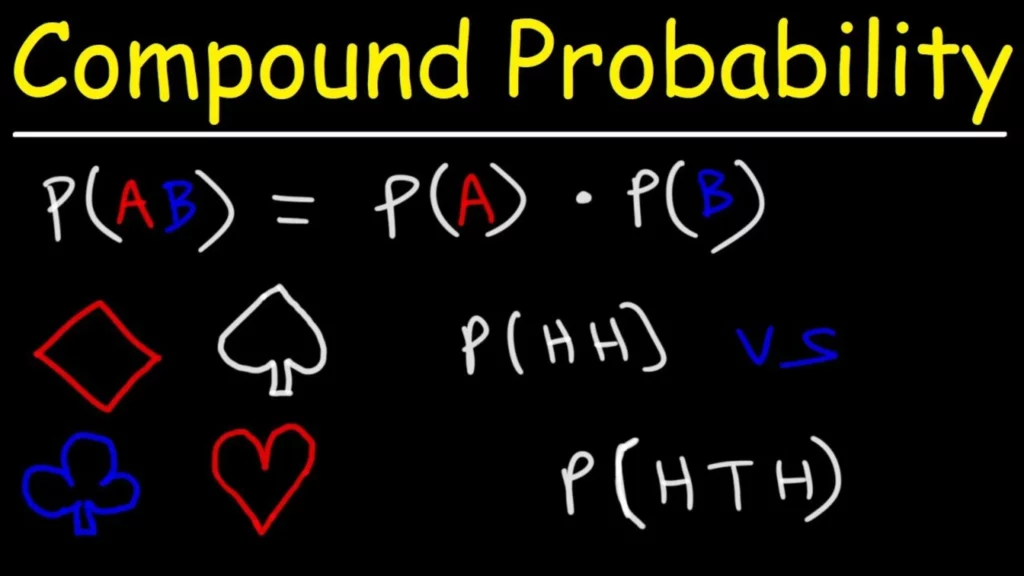
In simple terms, compound probability refers to the likelihood of two or more events occurring simultaneously. For instance, let’s say we have two events, A and B. The probability of event A occurring is P(A), and the probability of event B occurring is P(B). Now, if we want to calculate the probability of both events A and B occurring simultaneously, we need to calculate the compound probability of A and B, denoted as P(A and B).
Calculating Compound Probability
The formula for calculating compound probability depends on whether the events in question are independent or dependent. Independent events are those that do not affect the probability of each other. While dependent events are those that do. Let’s look at both scenarios in more detail.
Independent Events
When two events are independent, the probability of both events occurring is equal to the product of their individual probabilities. In other words:
P(A and B) = P(A) x P(B)
For instance, let’s say we have a bag containing five red marbles and three blue marbles. If we draw two marbles at random from the bag, what is the probability that both marbles will be red? The probability of drawing a red marble on the first draw is 5/8, and the probability of drawing another red marble on the second draw (assuming we don’t replace the first marble) is 4/7 (since there are now four red marbles left out of a total of seven marbles). Therefore, the compound probability of drawing two red marbles is:
P(drawing two red marbles) = P(Red on first draw) x P(Red on second draw)
P(drawing two red marbles) = (5/8) x (4/7)
P(drawing two red marbles) = 5/14
Dependent Events
When two events are dependent, the probability of both events occurring is equal to the product of the probability. The first event and the conditional probability of the second event given that the first event has already occurred. In other words:
P(A and B) = P(A) x P(B|A)
For instance, let’s say we have a deck of cards containing 52 cards, of which 26 are red and 26 are black. If we draw two cards at random from the deck without replacement, what is the probability that both cards will be red? The probability of drawing a red card on the first draw is 26/52 (or 1/2). But the probability of drawing another red card on the second draw is now 25/51. There are now only 25 red cards left out of a total of 51 cards. Therefore, the compound probability of drawing two red cards is:
P(drawing two red cards) = P(Red on the first draw) x P(Red on the second draw given that the first card was red)
P(drawing two red cards) = (26/52) x (25/51)
P(drawing two red cards) = 25/102
Applications of Compound Probability
Compound probability has many applications in real life. For instance, it can be used to calculate the likelihood of a certain medical condition occurring in a patient based on their age, gender, and family history. It can also be used in insurance and finance to calculate the probability of certain events, such as car accidents or stock market crashes.
Common Mistakes in Calculating Compound Probability
When calculating compound probability, it’s important to avoid some common mistakes that can lead to incorrect results. These include:
- Assuming that events are independent when they are actually dependent. This can happen when we overlook certain factors that can affect the probability of an event.
- Using the wrong formula for calculating compound probability. This can happen when we don’t pay attention to whether the events in question are independent or dependent.
- Assuming that the order of events doesn’t matter. In some cases, the order in which events occur can affect the probability of the outcome.
Finally
Compound probability is an important concept in probability theory that helps us calculate. The likelihood of multiple events occurring simultaneously. Whether we’re dealing with independent or dependent events, understanding how to calculate compound probability. It can help us make better decisions in various fields, from medicine to finance. By avoiding common mistakes and using the appropriate formula, we can improve our accuracy in predicting the likelihood of certain outcomes.



